Cấu kiá»n chá»u xoắn thÆ°á»ng có tiết diá»n Äặc (hình 3.23,a) hoặc tiết diá»n kÃn (hình 3.23,b,c). Trên mặt cắt ngang thanh chá» có ứng suất tiếp do mômen xoắn Mt gây ra:

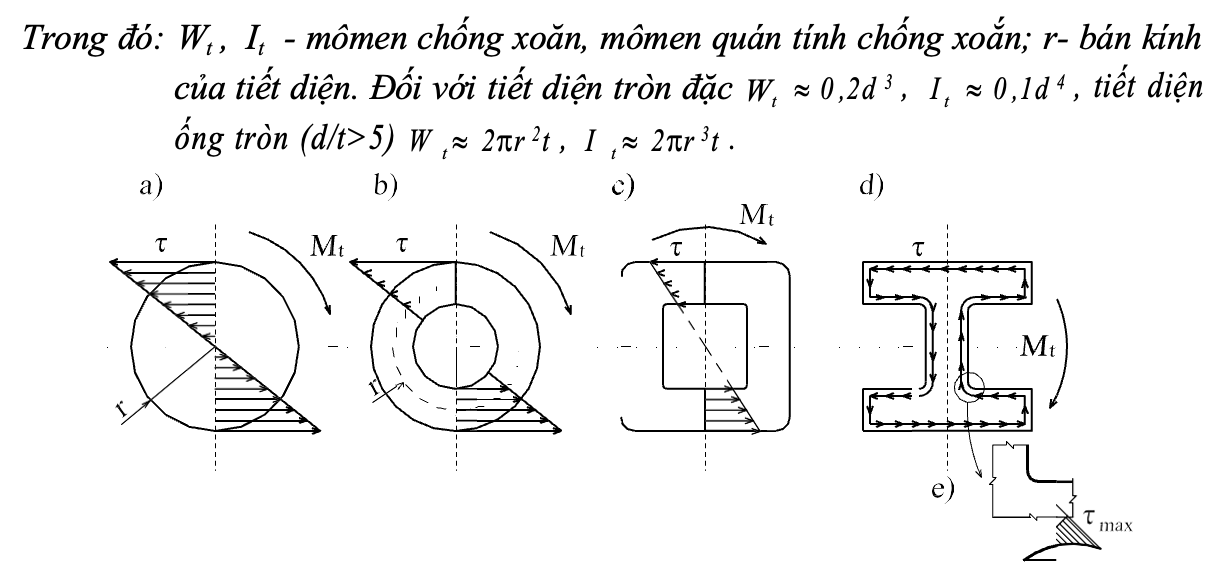
Hình 3.23. Phân bỠứng suất trong tiết diá»n cấu kiá»n chá»u xoắn: a-tiết diá»n Äặc; b, c â tiết diá»n kÃn; d- tiết diá»n há»; e-táºp trung ứng suất tại góc
Khi xoắn má»t thanh có tiết diá»n há» bất kỳ, nhÆ° tiết diá»n chữ I, C (h nh 3.23,d) It ï½ ï¡ ï¥ b t 3 / 3 , vá»i ï¡ là há» sá» Äiá»u chá»nh theo tiết diá»n: ï¡=1,3 Äá»i vá»i thép cán chữ I; ï¡=1,5 Äá»i vá»i dầm thép tá» hợp hà n có sÆ°á»n gia cÆ°á»ng; ï¡=1,12 Äá»i vá»i thép chữ C, ï¡=1,0 Äá»i vá»i thép góc.
Công thức (3.36) chÆ°a xét tá»i sá»± táºp trung ứng suất tại góc tiết diá»n (hình 3.23 ,e). Theo nghiên cứu của E.Treffsa [15], ứng suất tại Äó có thá» tÃnh nhÆ° sau:

Xoắn tá»± do (hình 3.24,a) các tiết diá»n xoay Äá»i vá»i nhau, các Äiá»m của tiết diá»n chuyá»n vá» không giá»ng nhau theo trục thanh. Tiết diá»n không còn phẳng nữa vÃ
sẽ vênh, Äó là sá»± vênh của tiết diá»n ngang. Nếu thanh có Äiá»u kiá»n sao cho má»i tiết diá»n ngang Äá»u vênh giá»ng nhau, tức là các thá» nằm giữa hai tiết diá»n ngang không bá» biến dạng, thì không có ứng suất pháp; ứng suất tiếp trong má»i tiết diá»n ngang là giá»ng nhau, còn gá»i là sá»± xoắn thuần túy.
Nếu do Äiá»u kiá»n liên kết gá»i tá»±a mà các tiết diá»n không thá» vênh tá»± do thì các thá» giữa hai tiết diá»n có những biến dạng dá»c khác nhau, sẽ xuất hiá»n ứng suất pháp và ứng suất tiếp phụ. Äó là sá»± xoắn kiá»m chế hay là xoắn uá»n vì có ứng suất pháp của sá»± uá»n.
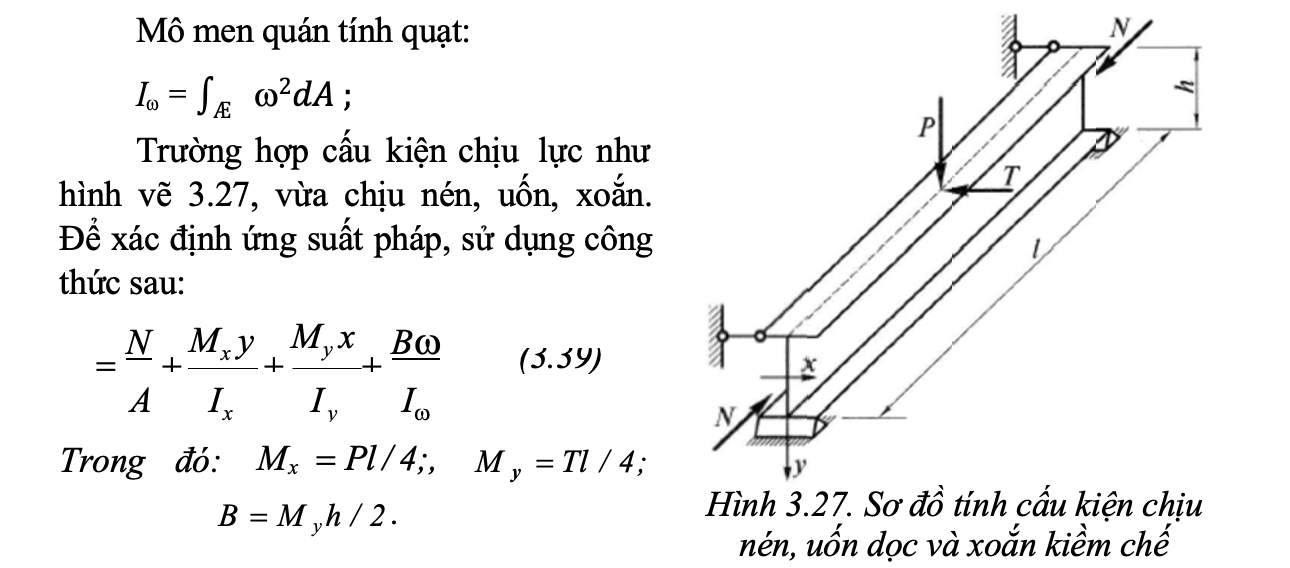
Và dụ thanh ngà m má»t Äầu (hình 3.24,b): tiết diá»n ngà m luôn luôn phẳng, cà ng xa cà ng vênh nhiá»u. Biến dạng dá»c của các thá» bá» hạn chế, là m xuất hiá»n ứng suất pháp và ứng suất tiếp phụ. Hai cánh bá» uá»n trong hai mặt phẳng theo 2 chiá»u khác nhau. Ứng suất pháp trong trÆ°á»ng hợp nà y:

Äá» nghiên cứu trạng thái ứng suất xoắn uá»n, ngoà i các Äặc trÆ°ng của thanh thÆ°á»ng, cần má»t sá» Äặc trÆ°ng hình há»c của tiết diá»n thanh má»ng há», xem xét á» dÆ°á»i Äây:
Bimômen xuất hiá»n khi xoắn kiá»m chế. Toà n bá» tiết diá»n quay quanh trục dá»c, má»i cánh dầm uá»n trong mặt phẳng của chúng. Trong má»i cánh có ứng suất uá»n, tạo nên 2 ngẫu lá»±c trong các mặt phẳng cánh, song song và cách nhau là h (chiá»u cao tiết diá»n) (hình 3.25).
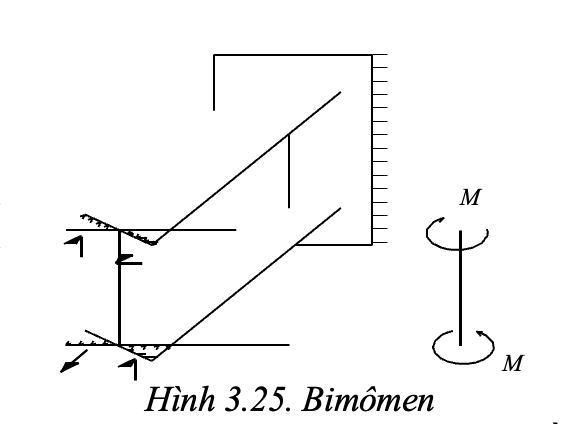
TÃch của M nà y vá»i khoảng cách giữa chúng gá»i là Bimômen B, là má»t há» gá»m 4 lá»±c (2 cặp ngẫu lá»±c) tá»± cân bằng nhau nên trong các phÆ°Æ¡ng trình cân bằng không xuất hiá»n và không xác Äá»nh Äược, muá»n tìm nó phải xác Äá»nh qua biá»u thức của góc xoắn ï±(z) là hà m của tá»a Äá» z.
Khái niá»m tá»a Äá» quạt. Xét tiết diá»n há», tâm O. Ox và Oy là trục quán tÃnh chÃnh trung tâm.
Trên hình 3.26, chá»n má»t Äiá»m A gá»i là cá»±c. Má»t bán kÃnh vectÆ¡ tùy ý AM0 là m bán kÃnh ban Äầu. Äiá»m M(x,y) bất kỳ trên ÄÆ°á»ng trung bình của tiết diá»n, bán kÃnh AM là bán kÃnh chạy. Hai lần diá»n tÃch quạt AMM0 gá»i là tá»a Äá» quạt ï· của Äiá»m M.
Quy Æ°á»c dấu ï· là dÆ°Æ¡ng nếu quét từ AM0 Äến bán kÃnh chạy theo chiá»u kim Äá»ng há». Váºy má»t Äiá»m M là có 3 tá»a Äá» x, y và ï·. Lấy bán kÃnh AM0 ngắn nhất gá»i là bán kÃnh ban Äầu chÃnh; Äiá»m M0 gá»i là Äiá»m quạt chÃnh. Lại chá»n Äiá»m A sao cho Iï·x và Iï·y bằng 0, A gá»i là cá»±c quạt.
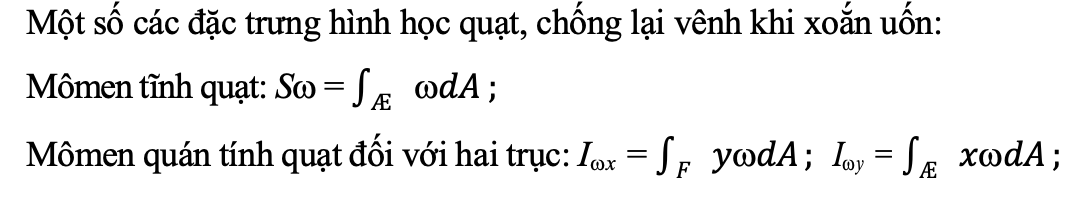
|
|
